كتاب روابط اجتياز لـ E. CVA Capital Formula
E. CVA Capital Formula
C 52/2017 GUI يسري تنفيذه من تاريخ 1/4/202120. In the BCBS publication of Basel III, banks using the standardised approach to calculate CVA capital are to use the following formula:
21. The Central Bank’s CVA calculation, while based directly on the BCBS formula and producing the same result, uses different (generally simpler) notation. The nature of, and motivation for, the main notational differences are explained in this section.
22. A minor difference in notation is the omission of the multiplicative term “![]() ” from the BCBS formulation. This term was included by the BCBS to allow the CVA capital calculation to be adjusted to an appropriate prudential horizon. However, in the ultimate calibration of the CVA calculation the horizon h was established at one year, and hence h=1. Since the square root of 1 is also 1, and the term is a multiplicative factor, it has no impact on the resulting capital. Some other jurisdictions have recognized this fact, and have omitted the
” from the BCBS formulation. This term was included by the BCBS to allow the CVA capital calculation to be adjusted to an appropriate prudential horizon. However, in the ultimate calibration of the CVA calculation the horizon h was established at one year, and hence h=1. Since the square root of 1 is also 1, and the term is a multiplicative factor, it has no impact on the resulting capital. Some other jurisdictions have recognized this fact, and have omitted the ![]() from the CVA calculation for simplicity in their published capital regulations. The Central Bank has followed this approach.
from the CVA calculation for simplicity in their published capital regulations. The Central Bank has followed this approach.
23. Another difference between the BCBS notation and the presentation of the formula in the Standards is the concept of “single-name exposure” or SNE. Under the Standards, a bank calculates SNE for each counterparty as:
SNEi = EADiTotal × DFi − Hi × DFH
In this calculation, EADiTotal is the bank’s total exposure to counterparty “i” across all derivatives netting sets plus the counterparty exposure measure arising from SFTs with that counterparty, and Hi is the total notional of eligible single-name CVA hedges for that counterparty. (The symbol H is used in place of B in the BCBS formula, an appropriate adjustment of notation since it reflects hedge instruments. DF is a supervisory discount factor, described further below.) In effect, the discounted value of the individual counterparty exposure is offset by the discounted value of eligible single-name CVA hedges for that counterparty. The Central Bank regards SNE as a useful concept, because it reflects single-name exposure net of hedges. Its use also simplifies presentation of the CVA capital formulas.
24. The form of the supervisory discount factor DF in the Standards differs somewhat from the corresponding BCBS notation. Specifically, DF is defined in the CVA Standards as:
This form of DF is in effect the continuous-time present value of an M-period annuity of one AED discounted at a rate of 5%.
25. In contrast, the BCBS formula includes the maturity term M directly in the denominator of the supervisory discount factor, as follows:
However, the BCBS formula for CVA capital also multiplies by M as part of the CVA capital calculation. As a result of that multiplication, the M in the denominator of the discount factor is cancelled out, making the overall result the same as that provided by DF in the Standards. The formulation in the BCBS text was designed to accommodate the fact that banks using internal models incorporate discounting into the calculation of counterparty exposure, and those banks are required to set the BCBS supervisory discount factor to one, while retaining the multiplication by M. However, since internal-model approaches are not used for regulatory capital purposes in the UAE, this flexibility is not needed, and the simpler version of the calculation has been specified in the Standards. If for operational or other reasons a bank finds using the Basel formulation of the discount factor more convenient, its use is acceptable, provided the bank also multiplies the resulting discount factor by M.
26. If the bank uses single-name hedging only, the bank aggregates SNE across counterparties to calculate CVA capital using the following formula:
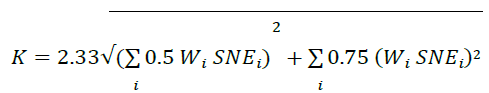
where K is CVA capital, and Wi is the risk weight applicable to counterparty “i” taken from the risk-weight table in the Standards.
27. An important insight is that CVA risk has both a systematic component and an idiosyncratic component. The systematic component reflects the fact that credit risks of different counterparties tend to be at least somewhat correlated with one another and move in concert, due to a degree of dependence on the same general economic or market factors. This kind of common risk potentially can be hedged, but cannot be reduced through diversification across counterparties. The non-systematic, or idiosyncratic, component of CVA risk arises from factors that affect credit spreads but are specific to an individual counterparty. In contrast to the systematic risk, the idiosyncratic part of CVA risk can be reduced through diversification, as well as through hedging. If a CVA portfolio is diversified to include many counterparties, it is not very likely that they would all suffer idiosyncratic credit deterioration at the same time, so overall risk is reduced; gains on some may offset losses on others.
28. The CVA capital calculation recognizes the difference between these two kinds of risk, and treats them differently in the calculation. The first term in the square root in the capital calculation reflects the systematic component of CVA variance:
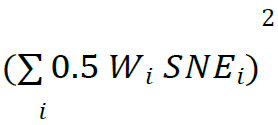
The exposures are weighted and summed before squaring. Holding risk weights constant, spreading a given amount of exposure across more counterparties has no effect on this sum; although there will be more individual terms in the summation, the sum will be the same, and thus there are no gains from diversification. The second term in the square root reflects the idiosyncratic CVA risk:
Here, because the weighted exposures are squared before summing, spreading a given amount of exposure across more counterparties reduces the total, reflecting the beneficial, risk-reducing effects of diversifying the idiosyncratic component of counterparty credit risk.
29. An alternative arrangement of the CVA capital calculation may provide additional intuition:
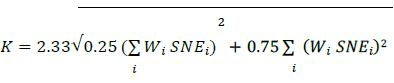
This form, which separates the factor of 0.5 from the rest of the systematic portion before it is raised to the second power, highlights the fact that the CVA calculation can be viewed as effectively a weighted average of two components, a systematic component with a weight of 25%, and an idiosyncratic component with a weight of 75%. The 25% weight on the idiosyncratic component is the theoretically correct weight if counterparties have a common systematic correlation with the broader market of 50%. Note that this form is simply a mathematical restatement of the capital calculation, yielding an identical answer for the stated case (that is, single-name hedging only, no index hedges).
30. The portfolio-level calculation of CVA risk also recognizes that index hedges may reduce systematic CVA risk. The calculation including index hedges is:
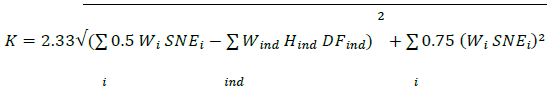
where Hind is the notional of an eligible purchased index hedge instrument that is used to hedge CVA risk, ![]() is the applicable supervisory discount factor, and Mind is the maturity of the index hedge. Note that the effect of the index hedge appears only in the systematic component of CVA risk within the square root. Also, note that there is no correlation-related coefficient associated with the index hedges, analogous to the 0.5 or 0.75 coefficients for the single-name exposure terms. This reflects the fact that an index CDS closely tracks the market, with a correlation expected to be near perfect. The correct coefficient on the index hedge terms in the model would be approximately 1.0, which is the reason for their omission.
is the applicable supervisory discount factor, and Mind is the maturity of the index hedge. Note that the effect of the index hedge appears only in the systematic component of CVA risk within the square root. Also, note that there is no correlation-related coefficient associated with the index hedges, analogous to the 0.5 or 0.75 coefficients for the single-name exposure terms. This reflects the fact that an index CDS closely tracks the market, with a correlation expected to be near perfect. The correct coefficient on the index hedge terms in the model would be approximately 1.0, which is the reason for their omission.
31. The Standards also includes a version of the formula that more closely resembles the full formula used in the BCBS framework:
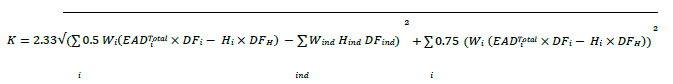
In this form, the intermediate calculation of SNE is not used. However, the results of the calculation are exactly the same as those produced by the formulation using SNE.