II. Clarifications
A. Replacement Cost
17.Note that in mathematical terms, replacement cost for un-margined transactions is calculated as:
RC = max(V − C; 0)
where RC is replacement cost, V is the total current market value of all derivative contracts in the netting set combined, and C is the net value of collateral for the netting set, after application of relevant haircuts. (In the CCR Standards, the quantity V-C is referred to as the Net Current Value, or NCV.)
18.For margined transactions, the calculation becomes:
RC = max(V − C; TH + MTA − NICA; 0)
where TH is the threshold level of variation that would require a transfer of collateral, MTA is the minimum transfer amount of the collateral, and NICA is the Net Independent Collateral Amount equal to the difference between the value of any independent collateral posted by a counterparty and any independent collateral posted by the bank for that counterparty, excluding any collateral that the bank has posted to a segregated, bankruptcy remote account.
19.When determining the RC component of a netting set, the netting contract must not contain any clause which, in the event of default of a counterparty, permits a non-defaulting counterparty to make limited payments only, or no payments at all, to the estate of the defaulting party, even if the defaulting party is a net creditor.
B. Netting
20.The Standards requires that a bank should apply netting only when it can satisfy the Central Bank that netting is appropriate, according to the specific requirements established in the Standards. Banks should recognize that this requirement would likely be difficult to meet in the case of trades conducted in jurisdictions lacking clear legal recognition of netting, which at present is the case in the UAE.
21.If netting is not recognized, then netting sets still should be used for the calculation. However, since each netting set must contain only trades that can be netted, each netting set is likely to consist of a single transaction. The calculations of EAD can still be performed, although they simplify considerably.
22.Note that there may be more than one netting set for a given counterparty. In that case, the CCR calculations should be performed for each netting set individually. The individual netting set calculations can be aggregated to the counterparty level for reporting or other purposes.
C. PFE Multiplier
23.For the multiplier of the PFE component, when the collateral held is less than the net market value of the derivative contracts (“under-collateralization”), the current replacement cost is positive and the multiplier is equal to one (i.e. the PFE component is equal to the full value of the aggregate add-on). Where the collateral held is greater than the net market value of the derivative contracts (“over-collateralization”), the current replacement cost is zero and the multiplier is less than one (i.e. the PFE component is less than the full value of the aggregate add-on).
D. Supervisory Duration
24.The Supervisory Duration calculation required in the Standards is in effect the present value of a continuous-time annuity of unit nominal value, discounted at a rate of 5%. The implied annuity is received between dates S and E (the start date and the end date, respectively), and the present value is taken to the current date.
25.For interest rate and credit derivatives, the supervisory measure of duration depends on each transaction’s start date S and end date E. The following Table presents example transactions and illustrates the values of S and E, expressed in years, which would be associated with each transaction, together with the maturity M of the transaction.
26.Note there is a distinction between the period spanned by the underlying transaction and the remaining maturity of the derivative contract. For example, a European interest rate swaption with expiry of 1 year and the term of the underlying swap of 5 years has S=1 year and E=6 years. An interest rate swap, or an index CDS, maturing in 10 years has S=0 years and E=10 years. The parameters S and E are only used for interest rate derivatives and credit-related derivatives.
E. Aggregation of Maturity Category Effective Notional Amounts
27.The Standards allows banks to choose between two options for aggregating the effective notional amounts that are calculated for each maturity category for interest rate derivatives. The primary formula is the following:
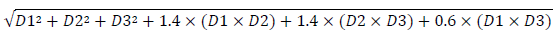
28.In this formula, D1 is the effective notional amount for maturity category 1, D2 is the effective notional amount for maturity category 2, and D3 is the effective notional amount for maturity category 3. As defined in the Standards, maturity category 1 is less than one year, maturity category 2 is one to five years, and maturity category 3 is more than five years.
29.As an alternative, the bank may choose to combine the effective notional values as the simple sum of the absolute values of D1, D2, and D3 within a hedging set, which has the effect of ignoring potential diversification benefits. That is, as an alternative to the calculation above, the bank may calculate:
|D1| + |D2| + |D3|
This alternative is a simpler calculation, but is more conservative in the sense that it always produces a larger result. To see this, note that the two calculations would give identical results only if the values 1.4 and 0.6 in the first formula are replaced with the value 2.0. Since the actual coefficient values are smaller than 2.0, the first formula gives a smaller result than the second formula. Choosing the second formula is equivalent to choosing to use the first formula with the 1.4 and 0.6 values replaced by 2.0, increasing measured CCR exposure and therefore minimum required capital.
F. Maturity Factor
30.Note that the Standards requires the use of a standard 250-day trading or business year for the calculation of the maturity factor and the MPOR. The view of the Central Bank is that a single, standardised definition of one year for this purpose will enhance comparability across banks and over time. However, the BCBS has indicated that the number of business days used for the purpose of determining the maturity factor be calculated appropriately for each transaction, taking into account the market conventions of the relevant jurisdiction. If a bank believes that use of a different definition of one year is appropriate, or would significantly reduce its compliance burden, the bank may discuss the matter with bank supervisors.
G. Delta Adjustment
31.Supervisory delta adjustments reflect the fact that the notional value of a transaction is not by itself a good indication of the associated risk. In particular, exposure to future market movements depends on the direction of the transaction and any non-linearity in the structure.
32.With respect to direction, a derivative may be long exposure to the underlying risk factor (price, rate, volatility, etc.), in which case the value of the derivative will move in the same direction as the underlying – gaining value with increases, losing value with decreases – and the delta is positive to reflect this relationship. The alternative is that a derivative may be short exposure to the underlying risk factor, in which case the value of the derivative moves opposite to the underlying – losing value with increases, and gaining value with decreases – and thus the delta is negative.
33.The non-linearity effects are prominent with transactions that involve contingent payoffs or option-like elements. Options and CDOs are notable examples. For such derivative transactions, the impact of a change in the price of the underlying instrument is not linear or one-for-one. For example, with an option on a foreign currency, when the exchange rate changes by a given amount, the change in the value of the derivative – the option contract – will almost always be less than the change in the exchange rate. Moreover, the amount by which the change is less than one-for-one will vary depending on a number of factors, including the current exchange rate relative to the exercise price of the option, the time remaining to expiration of the option, and the current volatility of the exchange rate. Without an adjustment for that difference, the notional amounts alone would be misleading indications of the potential for counterparty credit risk.
34.The supervisory delta adjustments for all derivatives are presented in the table below, which is repeated from the CCR Standards. These adjustments are defined at the trade level, and are applied to the adjusted notional amounts to reflect the direction of the transaction and its non-linearity.
35.Note that the supervisory delta adjustments for the various option transactions are closely related to the delta from the widely used Black-Scholes model of option prices, although the risk-free interest rate – which would ordinarily appear in this expression – is not included. In general, banks should use a forward price or rate, ideally reflecting any interim cash flows on the underlying instrument, as P in the supervisory delta calculation.
36.The expression for the supervisory delta adjustment for CDOs is based on attachment and detachment points for any tranche of the CDO. The precise specification (including the values of the embedded constants of 14 and 15) is the result of an empirical exercise conducted by the Basel Committee on Banking Supervision to identify a relatively simple functional form that would provide a sufficiently close fit to CDO sensitivities as reported by a set of globally active banks.
Supervisory Delta Adjustments
Type of Derivative Transaction Supervisory Delta Adjustment Purchased Call Option F Purchased Put Option F-1 Sold Call Option -F Sold Put Option 1-F Purchased CDO Tranche (Long Protection) G Sold CDO Tranche (Short Protection) -G Any Other Derivative Type, Long in the Primary Risk Factor +1 Any Other Derivative Type, Short in the Primary Risk Factor -1 Definitions
For options:
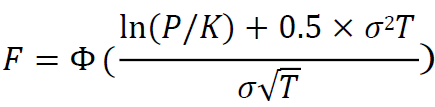
In this expression, P is the current forward value of the underlying price or rate, K is the exercise or strike price of the option, T is the time to the latest contractual exercise date of the option, σ is the appropriate supervisory volatility from Table 2, and Φ is the standard normal cumulative density function. A supervisory volatility of 50% should be used on swaptions for all currencies.
For CDO tranches:
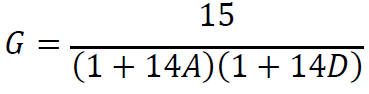
In this expression, A is the attachment point of the CDO tranche and D is the detachment point of the CDO tranche.
H. Complex Derivatives
37.The Standards requires that complex trades with more than one risk driver (e.g. multi-asset or hybrid derivatives) must be allocated to more than one asset class when the material risk drivers span more than one asset class. The full amount of the trade must be included in the PFE calculation for each of the relevant asset classes. Asset-class allocation of complex derivatives is a point of national discretion in the Basel framework, and the Central Bank believes that requiring banks to identify such trades and allocate them accordingly places appropriate responsibility on banks that choose to engage in such trades.
38.Examples of derivatives that reference the basis between two risk factors and are denominated in a single currency (basis transactions) include three-month Libor versus six-month Libor, three-month Libor versus three-month T-Bill, one-month Libor versus OIS rate, or Brent Crude oil versus Henry Hub gas. These examples are provided as illustrations, and do not represent an exhaustive list.
39.Hedging sets for derivatives that reference the volatility of a risk factor (volatility transactions) must follow the same hedging set construction outlined in the Standards for derivatives in that asset class; for example, all equity volatility transactions form a single hedging set. Examples of volatility transactions include variance and volatility swaps, or options on realized or implied volatility.
I. Unrated Reference Assets
40.The supervisory factor for credit derivatives depends on the credit rating of the underlying reference asset. The Basel framework does not provide a specific treatment of unrated reference assets. The Central Bank believes that credit derivatives on unrated reference entities are likely to be rare. However, for the sake of completeness, the Standards requires that any such credit derivatives be treated in a manner that is broadly consistent with the treatment of unrated entities in other aspects of the risk-based capital framework, through use of a Supervisory Factor corresponding to BBB or BB ratings as described in the Standards.
41.For an entity for which a credit rating is not available, a bank should use the Supervisory Factor corresponding to BBB. However, where the exposure is associated with an elevated risk of default, the bank should use the Supervisory Factor for BB. In this context, “elevated risk of default” should also be understood to include instances in which it is difficult or impossible to assess adequately whether the exposure has high risk of loss due to default by the obligor. A bank trading credit derivatives referencing unrated entities should conduct their own analysis to examine this risk.
J. Commodity Derivatives
42.Note that the Standards defines the term “commodity type” for purposes of calculation of exposure for CCR. A commodity type is defined as a set of commodities with broadly similar risk drivers, such that the prices or volatilities of commodities of the same commodity type may reasonably be expected to move with similar direction and timing and to bear predictable relationships to one another. For example, a commodity type such as coal might include several types of coal, and a commodity type such as oil might include oil of different grades from different sources. The prices of commodities of a given type may not move precisely in lock step, but they are likely to move in the same direction at roughly the same time, due to their dependence on common forces in commodity markets. Long and short trades within a single commodity type can be fully offset.
43.For commodity derivatives, defining individual commodity types is operationally difficult. In fact, it is generally not possible to fully specify all relevant distinctions between commodity types, and as a result, a single commodity type is likely to include individual commodities that in practice differ to some extent in the dynamic behaviour they exhibit. As a result, not all basis risk is likely to be captured. Nonetheless, banks should attempt to minimize unrecognized basis risk through sound definitions of commodity types.
44.The Standards requires a bank to establish appropriate governance processes for the creation and maintenance of the list of defined commodity types used by the bank for CCR calculations, with clear definitions and independent internal review or validation processes to ensure that commodities grouped as a single type are in fact similar. A bank can only use the specifically defined commodity types it has established through its adequately controlled internal processes.
45.Trades within the same commodity hedging set (Energy, Metals, Agriculture, and Other) enjoy partial offsetting through the use of correlation values established in the Standards, with correlation values varying by asset subclass. More specifically, partial offsetting applies only to the systematic component, not the issuer-specific or idiosyncratic component. Note that Electricity is a sub-class of the Commodity asset class, but is itself part of the broader Energy hedging set, rather than constituting a distinct hedging set.
K. Single-Name and Index Derivatives
46.For credit derivatives, there is one credit reference entity for each reference debt instrument that underlies a single-name transaction allocated to the credit risk category. Single-name transactions should be assigned to the same credit reference entity only where the underlying reference debt instrument of those transactions is issued by the same issuer.
47.The approach for establishing the reference entity for equity derivatives should correspond to the general approach for credit derivatives.
48.For credit derivatives with indices as the underlying instrument, there should be one reference entity for each group of reference debt instruments or single-name credit derivatives that underlie a multi-name transaction. Multi-name transactions should be assigned to the same credit reference entity only where the group of underlying reference debt instruments or single-name credit derivatives of those transactions has the same constituents. The determination of whether an index is investment grade or speculative grade should be based on the credit quality of the majority of its individual constituents.
49.Again, the approach for equity index derivatives should follow the general approach for credit index derivatives.
L. Special Cases of Margin Agreements
50.When multiple margin agreements apply to a single netting set, the netting set should be broken down into sub-netting sets that align with the respective margin agreement for calculating both RC and PFE.
51.When a single margin agreement applies to multiple netting sets, RC at any given time is determined by the sum of two terms. The first term is equal to the un-margined current exposure of the bank to the counterparty aggregated across all netting sets within the margin agreement reduced by the positive current net collateral (i.e. collateral is subtracted only when the bank is a net receiver of collateral). The second term is non-zero only when the bank is a net poster of collateral: it is equal to the current net posted collateral (if there is any) reduced by the un-margined current exposure of the counterparty to the bank aggregated across all netting sets within the margin agreement. Net collateral available to the bank should include both VM and NICA. Mathematically, RC for the entire margin agreement is:
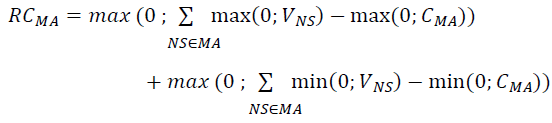
where the summation NS ∈ MA is across the netting sets covered by the margin agreement (hence the notation), VNS is the current mark-to-market value of the netting set NS and CMA is the cash equivalent value of all currently available collateral under the margin agreement.
52.An alternative description of this calculation is as follows:
Step 1: Compute the net value, positive or negative, of each netting set. These calculated values correspond to the terms VNS in the expression above.
Step 2: Sum the values of all netting sets with positive value, to get Total Positive Value (TPV). This corresponds to the term in the expression above: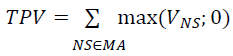
Step 3: Sum the values of all of netting sets with negative value, to get Total Negative Value (TNV). This corresponds to the term in the expression above: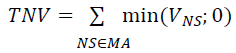
Step 4: Calculate the net current cash value of collateral, including NICA and VM. This corresponds to the term CMA in the expression above. If the bank is net holder of collateral, then CMA is positive; it is the net value held (NVH). If the bank is a net provider of collateral, then CMA is negative, and its absolute value is the net value provided (NVP). Note that either NVH>0 and NVP=0, or NVP>0 and NVH=0.
One of the following cases then applies:
Step 5a: If NVH>0 (so NVP=0), then RC = TPV – NVH, but with a minimum of zero – that is, RC cannot be negative.
or
Step 5b: If NVH=0 (so NVP>0), then RC = TPV + NVP – TNV, but with a minimum of TPV – that is, RC cannot be less than TPV.
53.To calculate PFE when a single margin agreement applies to multiple netting sets, netting set level un-margined PFEs should be calculated and aggregated, i.e. PFE should be calculated as the sum of all the individual netting sets considered as if they were not subject to any form of margin agreement.
