II. Clarifications
A. Scope
7. The CVA standards covers all of a bank’s non-centrally cleared derivative exposures. In the context of the CVA standards, derivatives are instruments whose value is based upon the price or value associated with an underlying reference entity. In general, derivatives exhibit the following abstract characteristics:
- The transactions generate a current exposure or market value.
- The transactions have an associated random future market value based on market variables.
- The transactions have contractual terms that provide for an exchange of payments or an exchange of a financial instrument (including commodities) against payment.
- The transactions are undertaken with an identified counterparty.
8. Other common characteristics of derivative transactions may include the following:
- Collateral may be used to mitigate risk exposure, and may be inherent in the nature of some transactions.
- Netting may be used to mitigate risk or to simplify operational aspects of the transaction.
- Positions are frequently valued (most commonly on a daily basis), with the value dependent on market variables or their changes.
- Margin payments may be employed, with margin held in various forms, and with re-margining agreements that allow for the adjustment of margin either daily or at some other established frequency.
9. In addition, the Central Bank has used national discretion to include securities financing transactions (SFTs) – transactions such as repurchase agreements, reverse repurchase agreements, security lending and borrowing, and margin lending transactions – within the scope of the CVA calculation. However, as the Standards note, if the Central Bank determines that SFT exposures at any individual bank are not a material source of CVA risk, the Central Bank may direct the bank to exclude SFTs from CVA capital calculations.
10. Consistent with the BCBS framework, all derivative transactions for which a central counterparty is the direct counterparty are excluded from the CVA capital calculation. Banks must calculate RWA for those centrally cleared transactions as specified in the Central Bank’s CCR Standards.
B. CVA Overview
11.The Central Bank’s approach to minimum required capital for CVA risk is based closely on the standardised approach to CVA risk capital described in Basel III: A global regulatory framework for more resilient banks and banking systems (BCBS 189, December 2010, rev June 2011). A few elements also draw on clarifications and other information provided in BCBS publications responding to Frequently Asked Questions, or clarifications contained in Basel III: Finalising post-crisis reforms published by the BCBS in December 2017.
12.Regulatory CVA may differ from the CVA calculated under IFRS or other accounting standards. In particular, regulatory CVA excludes any consideration of the effect of changes in a bank’s own credit risk as perceived by the market. This means that regulatory CVA calculations do not consider so-called debit valuation adjustments, or DVA.
C. Hedging
13.The calculation allows banks to recognize the risk mitigating benefits of certain eligible CVA hedges. The Standards allows only certain types of instruments to serve as eligible hedges for CVA, specifically an index credit default swap (CDS), or a single-name CDS, single-name contingent CDS, or equivalent hedging instrument that directly references the counterparty being hedged. An option on an eligible CDS (that is, a swaption on such a CDS) can be eligible, provided the swaption does not contain a “knock out” clause that terminates the swaption in the case of a credit event. Eligible hedges that are included in the CVA capital charge are removed from the bank’s market risk capital calculation.
14.Other types of instruments must not be reflected as hedges within the calculation of the CVA capital charge, even if the bank views them as mitigating counterparty credit risk. For example, tranched or nth-to-default CDS instruments are not eligible CVA hedges. These instead must be treated as any other similar instrument in the bank’s portfolio for regulatory capital purposes.
15.In addition to the restrictions regarding the types of instruments that a bank may recognize as CVA hedges, only transactions entered into explicitly for the purpose of hedging the counterparty credit spread component of CVA risk can be eligible hedges. This means, for example, that a bank might have a single-name CDS referencing an OTC counterparty in its portfolio, and yet that CDS would not be eligible to offset the single-name CVA exposure within the CVA calculation if that CDS was not originated or acquired as part of the bank’s process to manage CVA risk for that particular counterparty.
16.To clearly demonstrate intent to manage CVA risk, the bank should have a documented CVA risk management process or program, so that any CVA hedging transaction is demonstrably consistent with the design and operation of that program, was entered into with the intent to mitigate the counterparty credit spread component of CVA risk, and continues to be managed by the bank in a manner consistent with that intent. The Central Bank expects that any bank wishing to recognize the benefits of hedges in CVA capital calculations will maintain policies and procedures to govern this process. If the Central Bank concludes that a bank’s CVA hedging policies and procedures are inadequate, the Central Bank may limit the bank’s ability to recognize hedges in CVA capital calculations.
17.Another key principle for CVA hedging is that risk mitigation should transfer risk to third parties external to the bank. Some banks use internal transactions to transfer risk between different desks or business units within the bank as part of a broader risk management program, with these transactions typically subject to some type of internal transfer pricing mechanism. Such transactions are permissible and can be a valid component of the management of CVA risk within a bank, but the risk ultimately should be transferred out of the bank, which generally requires a corresponding external transaction to reduce CVA risk.
D. CVA Capital Concept
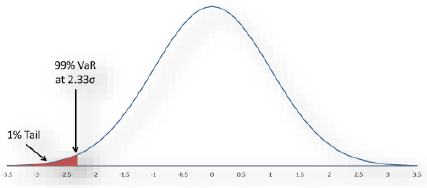
18.The standardised approach for calculation of CVA capital is a form of a value-at-risk calculation, an approach commonly used to set capital requirements. Changes in CVA can be viewed as following some distribution, such as the normal distribution illustrated in Figure 2. Conceptually, the general approach to CVA capital is to estimate a level of CVA losses that should be expected to be exceeded no more than a given percentage of the time. The CVA capital calculation reflects a value-at-risk calculation with a one-year, 99% confidence level for CVA risk. Assuming a normal distribution (or equivalently, a log-normal distribution for the underlying risk factors), losses can be expected to be within 2.33 standard deviations of the mean 99% of the time. That concept is illustrated in Figure 2, where the 1% negative tail of the distribution has been highlighted (in this case, σ is the standard deviation).
Figure 2

19. Accordingly, the general form of the CVA capital calculation depends on the standard deviation of CVA losses:
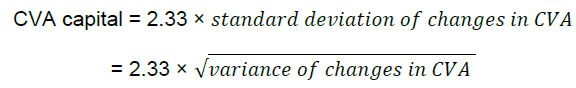
The normality assumption, together with a desired 99% confidence level, is the reason for the inclusion of a 2.33 multiplication factor in the CVA capital formula. Other elements of the CVA capital calculation reflect a theoretical approximation of the variance of changes in CVA.
E. CVA Capital Formula
20. In the BCBS publication of Basel III, banks using the standardised approach to calculate CVA capital are to use the following formula:
21. The Central Bank’s CVA calculation, while based directly on the BCBS formula and producing the same result, uses different (generally simpler) notation. The nature of, and motivation for, the main notational differences are explained in this section.
22. A minor difference in notation is the omission of the multiplicative term “
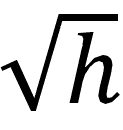 ” from the BCBS formulation. This term was included by the BCBS to allow the CVA capital calculation to be adjusted to an appropriate prudential horizon. However, in the ultimate calibration of the CVA calculation the horizon h was established at one year, and hence h=1. Since the square root of 1 is also 1, and the term is a multiplicative factor, it has no impact on the resulting capital. Some other jurisdictions have recognized this fact, and have omitted the
” from the BCBS formulation. This term was included by the BCBS to allow the CVA capital calculation to be adjusted to an appropriate prudential horizon. However, in the ultimate calibration of the CVA calculation the horizon h was established at one year, and hence h=1. Since the square root of 1 is also 1, and the term is a multiplicative factor, it has no impact on the resulting capital. Some other jurisdictions have recognized this fact, and have omitted the 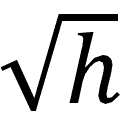 from the CVA calculation for simplicity in their published capital regulations. The Central Bank has followed this approach.
from the CVA calculation for simplicity in their published capital regulations. The Central Bank has followed this approach.23. Another difference between the BCBS notation and the presentation of the formula in the Standards is the concept of “single-name exposure” or SNE. Under the Standards, a bank calculates SNE for each counterparty as:
SNEi = EADiTotal × DFi − Hi × DFH
In this calculation, EADiTotal is the bank’s total exposure to counterparty “i” across all derivatives netting sets plus the counterparty exposure measure arising from SFTs with that counterparty, and Hi is the total notional of eligible single-name CVA hedges for that counterparty. (The symbol H is used in place of B in the BCBS formula, an appropriate adjustment of notation since it reflects hedge instruments. DF is a supervisory discount factor, described further below.) In effect, the discounted value of the individual counterparty exposure is offset by the discounted value of eligible single-name CVA hedges for that counterparty. The Central Bank regards SNE as a useful concept, because it reflects single-name exposure net of hedges. Its use also simplifies presentation of the CVA capital formulas.
24. The form of the supervisory discount factor DF in the Standards differs somewhat from the corresponding BCBS notation. Specifically, DF is defined in the CVA Standards as:
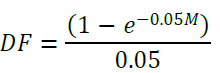
This form of DF is in effect the continuous-time present value of an M-period annuity of one AED discounted at a rate of 5%.
25. In contrast, the BCBS formula includes the maturity term M directly in the denominator of the supervisory discount factor, as follows:
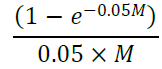
However, the BCBS formula for CVA capital also multiplies by M as part of the CVA capital calculation. As a result of that multiplication, the M in the denominator of the discount factor is cancelled out, making the overall result the same as that provided by DF in the Standards. The formulation in the BCBS text was designed to accommodate the fact that banks using internal models incorporate discounting into the calculation of counterparty exposure, and those banks are required to set the BCBS supervisory discount factor to one, while retaining the multiplication by M. However, since internal-model approaches are not used for regulatory capital purposes in the UAE, this flexibility is not needed, and the simpler version of the calculation has been specified in the Standards. If for operational or other reasons a bank finds using the Basel formulation of the discount factor more convenient, its use is acceptable, provided the bank also multiplies the resulting discount factor by M.
26. If the bank uses single-name hedging only, the bank aggregates SNE across counterparties to calculate CVA capital using the following formula:
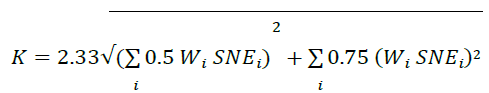
where K is CVA capital, and Wi is the risk weight applicable to counterparty “i” taken from the risk-weight table in the Standards.
27. An important insight is that CVA risk has both a systematic component and an idiosyncratic component. The systematic component reflects the fact that credit risks of different counterparties tend to be at least somewhat correlated with one another and move in concert, due to a degree of dependence on the same general economic or market factors. This kind of common risk potentially can be hedged, but cannot be reduced through diversification across counterparties. The non-systematic, or idiosyncratic, component of CVA risk arises from factors that affect credit spreads but are specific to an individual counterparty. In contrast to the systematic risk, the idiosyncratic part of CVA risk can be reduced through diversification, as well as through hedging. If a CVA portfolio is diversified to include many counterparties, it is not very likely that they would all suffer idiosyncratic credit deterioration at the same time, so overall risk is reduced; gains on some may offset losses on others.
28. The CVA capital calculation recognizes the difference between these two kinds of risk, and treats them differently in the calculation. The first term in the square root in the capital calculation reflects the systematic component of CVA variance:
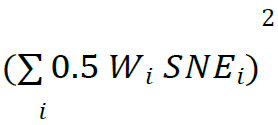
The exposures are weighted and summed before squaring. Holding risk weights constant, spreading a given amount of exposure across more counterparties has no effect on this sum; although there will be more individual terms in the summation, the sum will be the same, and thus there are no gains from diversification. The second term in the square root reflects the idiosyncratic CVA risk:
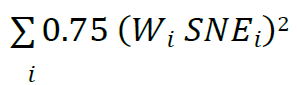
Here, because the weighted exposures are squared before summing, spreading a given amount of exposure across more counterparties reduces the total, reflecting the beneficial, risk-reducing effects of diversifying the idiosyncratic component of counterparty credit risk.
29. An alternative arrangement of the CVA capital calculation may provide additional intuition:
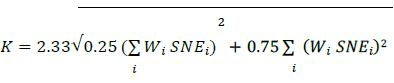
This form, which separates the factor of 0.5 from the rest of the systematic portion before it is raised to the second power, highlights the fact that the CVA calculation can be viewed as effectively a weighted average of two components, a systematic component with a weight of 25%, and an idiosyncratic component with a weight of 75%. The 25% weight on the idiosyncratic component is the theoretically correct weight if counterparties have a common systematic correlation with the broader market of 50%. Note that this form is simply a mathematical restatement of the capital calculation, yielding an identical answer for the stated case (that is, single-name hedging only, no index hedges).
30. The portfolio-level calculation of CVA risk also recognizes that index hedges may reduce systematic CVA risk. The calculation including index hedges is:
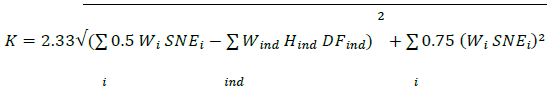
where Hind is the notional of an eligible purchased index hedge instrument that is used to hedge CVA risk,
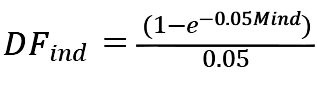 is the applicable supervisory discount factor, and Mind is the maturity of the index hedge. Note that the effect of the index hedge appears only in the systematic component of CVA risk within the square root. Also, note that there is no correlation-related coefficient associated with the index hedges, analogous to the 0.5 or 0.75 coefficients for the single-name exposure terms. This reflects the fact that an index CDS closely tracks the market, with a correlation expected to be near perfect. The correct coefficient on the index hedge terms in the model would be approximately 1.0, which is the reason for their omission.
is the applicable supervisory discount factor, and Mind is the maturity of the index hedge. Note that the effect of the index hedge appears only in the systematic component of CVA risk within the square root. Also, note that there is no correlation-related coefficient associated with the index hedges, analogous to the 0.5 or 0.75 coefficients for the single-name exposure terms. This reflects the fact that an index CDS closely tracks the market, with a correlation expected to be near perfect. The correct coefficient on the index hedge terms in the model would be approximately 1.0, which is the reason for their omission.31. The Standards also includes a version of the formula that more closely resembles the full formula used in the BCBS framework:
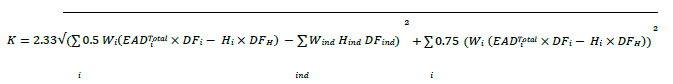
In this form, the intermediate calculation of SNE is not used. However, the results of the calculation are exactly the same as those produced by the formulation using SNE.
F. Maturity Calculation
32.When computing the maturity M for a netting set, banks are required to use a weighted average, with notional values as the weights. For example, suppose a netting set with a particular counterparty includes two exposures, a 2-year swap with a notional amount of 200, and a 3-year swap with a notional amount of 400. The total notional value of the netting set is therefore 200+400=600. The weighted average maturity would be calculated as:
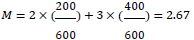
G. Risk Weights
33. Derivatives exposures and CVA hedges enter the CVA capital calculation with associated risk weights that depend on the credit rating of the bank’s counterparties for the covered exposures, or on the credit rating of the underlying entity for hedge instruments. In the case of unrated counterparties or entities, banks should follow the approach applied by the Central Bank for credit derivatives that reference unrated entities in the CCR Standards, treating them as BBB rated unless the counterparty or entity has an elevated risk of default, in which case they should be treated as BB rated.
34. The CVA Standards follows the BCBS framework in specifying an array of risk weights that align with an external rating scale that is most similar to the one used by Standard and Poor’s. Use of this rating scale for purposes of the CVA Standards should not be viewed as an endorsement of that or any other external rating agency. Banks may use other ratings, and should map those ratings to the scale included in the Standards using the historical default experience for the various rating grades as published by the relevant external rating agencies.
H. Risk-Weighted Assets
35. The formula developed by the BCBS to determine CVA capital reflects a calibration based on the 8% minimum capital ratio applied in the Basel capital framework. To calculate a corresponding RWA amount, the Standards requires banks to multiply the calculated CVA capital by a factor of 12.5, which is the reciprocal of 8%. That is, 1/(0.08) = 12.5. This multiplication is appropriate even if the Central Bank applies a higher minimum capital requirement to the resulting RWA, because the purpose of the multiplication by 12.5 is to reverse the calibration implicitly used by the BCBS to produce a capital number in the original formulation.
I. Threshold for the Simple Alternative
36.As part of the finalization of Basel III, the BCBS introduced a materiality threshold, and provided an option for any bank whose aggregate notional amount of non-centrally cleared derivatives is less than or equal to 100 billion euro to choose to set its CVA capital equal to 100% of its capital for counterparty credit risk.
37.To implement this option in the UAE, the Central Bank has established a materiality threshold of 400 billion AED. Banks with an aggregate notional amount of covered transactions less than or equal to 400 billion AED may choose to set CVA RWA equal to the bank’s RWA for counterparty credit risk as calculated under the Central Bank’s CCR Standards. The Central Bank has determined that this threshold is appropriate for the UAE, and is comparable to the 100 Billion Euro threshold included in Basel.
38.If a bank chooses this CDS, it must be applied to all of the bank’s covered transactions, as required under the BCBS framework. In addition, a bank adopting this simple approach may not recognize the risk-reducing effects of CVA hedges.
39.The Central Bank may prohibit a bank from using this simple alternative if the Central bank determines that CVA risk resulting from the bank’s derivative positions and SFTs materially contributes to the bank’s overall risk, and therefore warrants a more sophisticated approach.