3 PD Models
3.1 Scope
3.1.1
The majority of institutions employ models to estimate the probability of default of their obligors (or facilities), for risk management purpose and to comply with accounting and regulatory requirements. These models are generally referred to as ‘PD models’, although this broad definition covers several types of models. For the purpose of the MMG, and to ensure appropriate model management, the following components should be considered as separate models:
(i) Rating-to-PD mapping models, and (ii)
Point-in-Time PD Term Structure models.
3.1.2
These models have implications for key decisions including, but not limited to, risk management, provisioning, pricing, capital allocation and Pillar II capital assessment. Institutions should manage these models through a complete life-cycle process in line with the requirements articulated in the MMS. In particular, the development, ownership and validation process should be clearly organised and documented.
3.2 Key Definitions and Interpretations
3.2.1
The following definitions are complementing the definitions provided at the beginning of the MMG. The probability of default of a borrower or of a facility is noted “PD”. The loss proportion of exposure arising after default, or “loss given default” is noted “LGD”.
3.2.2
A point-in-time assessment (“PIT”) refers to the value of a metric (typically PD or LGD) that incorporates the current economic conditions. This contrasts with a through-the-cycle assessment (“TTC”) that refers to the value of the same metric across a period covering one or several economic cycles.
3.2.3
A PD is associated with a specific time horizon, which means that the probability of default is computed over a given period. A 1-year PD refers to the PD over a one year period, starting today or at any point in the future. A PD Term Structure refers to a cumulative PD over several years (generally starting at the portfolio estimation date). This contrasts with a marginal forward 1-year PD, which refers to a PD starting at some point in the future and covering a one year period, provided that the obligor has survived until that point.
3.2.4
A rating transition matrix is a square matrix that gives the probabilities to migrate from a rating to another rating. This probability is expressed over a specific time horizon, typically one year, in which case we refer to a ‘one-year transition matrix’. Transitions can also be expressed over several years.
3.3 Default Rate Estimation
3.3.1
Prior to engaging in modelling, institutions should implement a robust process to compute time series of historical default rates, for all portfolios where data is available. The results should be transparent and documented. This process should be governed and approved by the Model Oversight Committee. Once estimated, historical default rates time series should only be subject to minimal changes. Any retroactive updates should be approved by the Model Oversight Committee and by the bank’s risk management committee.
3.3.2
Institutions should estimate default rates at several levels of granularity: (i) for each portfolio, defined by obligor type or product, and (ii) for each rating grade within each portfolio, where possible. In certain circumstances, default rate estimation at rating grade level may not be possible and institutions may only rely on pool level estimation. In this case, institutions should justify their approach by demonstrating clear evidence based on data, that grade level estimation is not deemed sufficiently robust.
3.3.3
Institutions should compute the following default ratio, based on the default definition described in the previous section. This ratio should be computed with an observation window of 12 months to ensure comparability across portfolios and institutions. In addition, institutions are free estimate this ratio for other windows (e.g. quarterly) for specific modelling purposes.
(i)
The denominator is composed of performing obligors with any credit obligation, including off and on balance sheet facilities, at the start of the observation window. (ii) The numerator is composed of obligors that defaulted at least once during the observation window, on the same scope of facilities.
Formally the default rate can be expressed as shown by the formula below, where t represented the date of estimation. Notice that if the ratio is reported at time t, then the ratio is expressed as a backward looking metrics. This concept is particularly relevant for the construction of macro models as presented in subsequent sections. The frequency of computation should be at least quarterly and possibly monthly for some portfolios.
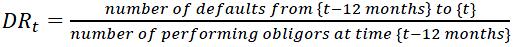
3.3.4
When the default rate is computed by rating grade, the denominator should refer to all performing obligors assigned to a rating grade at the beginning of the observation window. When the default rate is computed at segment level, the denominator should refer to all performing obligors assigned to that segment at the beginning of the observation window.
3.3.5
For wholesale portfolios, this ratio should be computed in order to obtain quarterly observations over long time periods covering one or several economic cycles. For wholesale portfolios, institutions should aim to gather at least 5 years of data, and preferably longer. For retail portfolios or for portfolios with frequent changes in product offerings, the period covered may be shorter, but justification should be provided.
3.3.6
Institutions should ensure that default time series are homogeneous and consistent through time, i.e. relate to a portfolio with similar characteristics, consistent lending standards and consistent definition of default. Adjustments may be necessary to build time series representative of the institution current portfolios. Particular attention should be given to changes in the institution’s business model through time. This is relevant is the case of rapidly growing portfolios or, conversely, in the case of portfolio run-off strategies. This point is further explained in the MMG section focusing on macro models.
3.3.7
If an obligor migrates between ratings or between segments during the observation period, the obligor should be included in the original rating bucket and/or original segment for the purpose of estimating a default rate. Institutions should document any changes in portfolio segmentation that occurred during the period of observation.
3.3.8
When the default rate is computed by rating grade, the ratings at the beginning of the observation window should not reflect risk transfers or any form of parent guaranties, in order to capture the default rates pertaining to the original creditworthiness of the obligors. The ratings at the start of the observation window can reflect rating overrides if these overrides relate to the obligors themselves, independently of guarantees.
3.3.9
When default rate series are computed over long time periods, it could happen that obligors come out of their default status after a recovery and a cure period. In subsequent observation windows, such obligors could be performing again and default again, in which case another default event should be recorded. For that purpose, institutions should define minimum cure periods per product and/or portfolio type. If a second default occurs after the end of the cure period, it should be recorded as an addition default event. These cure periods should be based on patterns observed in data sets.
3.3.10
Provided that institutions follow the above practices, the following aspects remain subject to the discretion of each institution. First, they may choose to exclude obligors with only undrawn facilities from the numerator and denominator to avoid lowering unduly the default rate of obligors with drawn credit lines. Second, institutions may also choose to estimate default rates based on exposures rather than on counts of obligors; such estimation provides additional statistical information on expected exposures at default.
3.4 Rating-to-PD
3.4.1
For the purpose of risk management, the majority of institutions employ a dedicated methodology to estimate a TTC PD associated with each portfolio and, where possible, associated with each rating grade (or score) generated by their rating models. This estimation is based on the historical default rates previously computed, such that the TTC PD reflects the institution’s experience.
3.4.2
This process results in the construction of a PD scale, whereby the rating grades (or scores) are mapped to a single PD master scale, often common across several portfolios. This mapping exercise is referred to as ‘PD calibration’. It relies on assumptions and methodological choices separate from the rating model, therefore it is recommended to considered such mapping as a standalone model. This choice is left to each institution and should be justified. The approach should be tested, documented and validated.
3.4.3
Institutions should demonstrate that the granularity of segmentation employed for PD modelling is an appropriate reflection of the risk profile of their current loan book. The segmentation granularity of PD models should be based on the segmentation of rating models. In other words, the segmentation of rating models should be used as a starting point, from which segments can be grouped or split further depending on portfolio features, provided it is fully justified. This modelling choice has material consequences on the quality of PD models; therefore, it should be documented and approved by the Model Oversight Committee. Finally, the choice of PD model granularity should be formally reviewed as part of the validation process.
3.4.4
The rating-to-PD mapping should be understood as a relationship in either direction since no causal relationship is involved. The volatility of the grade PD through time depends on the sensitivity of the rating model and on the rating methodology employed. Such volatility will arise from a combination of migrations across rating grades and changes in the DR observed for each grade. Two situations can arise:
(i)
If rating models are sensitive to economic conditions, ratings will change and the exposures will migrate across grades, while the DR will remain stable within each grade. In this case, client ratings will change and the TTC PD assigned to each rating bucket will remain stable. (ii)
If rating models are not sensitive to economic conditions, then the exposures will not migrate much through grades but the DR of each grade will change. In this case, client ratings will remain stable but the observed DR will deviate from the TTC PD assigned to each rating bucket.
3.4.5
Institutions should estimate the degree to which they are exposed to each of the situations above. Institutions are encouraged to favour the first situation, i.e. implement rating models that are sensitive to economic conditions, favour rating migrations and keep the 1-year TTC PD assigned to each rating relatively stable. For the purpose of provisioning, economic conditions should be reflected in the PIT PD in subsequent modelling. Deviation from this practice is possible but should be justified and documented.
3.4.6
The estimation of TTC PD relies on a set of principles that have been long established in the financial industry. At a minimum, institutions should ensure that they cover the following aspects:
(i)
The TTC PD associated with each portfolio or grade should be the long-run average estimation of the 1-year default rates for each corresponding portfolio or grade. (ii)
The DR time series should be homogeneous and consistent through time, i.e. relate to a portfolio with similar characteristics and grading method. (iii)
TTC PDs should incorporate an appropriate margin of conservatism depending on the time span covered and the population size. (iv)
TTC PDs should be estimated over a minimum of five (5) years and preferably longer for wholesale portfolios. For retail portfolios, changes in product offerings should be taken into account when computing TTC PD. (v)
The period employed for this estimation should cover at least one of the recent economic cycles in the UAE: (i) the aftermath of the 2008 financial crisis, (ii) the 2015-2016 economic slowdown after a sharp drop in oil price, and/or (iii) the Covid-19 crisis. (vi)
If the estimation period includes too many years of economic expansion or economic downturn, the TTD PD should be adjusted accordingly.
3.4.7
For low default portfolios, institutions should employ a separate approach to estimate PDs. They should identify an appropriate methodology suitable to the risk profile of their portfolio. It is recommended to refer to common methods proposed by practitioners and academics to address this question. Amongst others, the Pluto & Tasche method or the Benjamin, Cathcart and Ryan method (BCR) are suitable candidates.
3.4.8
For portfolios that are externally rated by rating agencies, institutions can use the associated TTC PDs provided by rating agencies. However, institutions should demonstrate that (i) they do not have sufficient observed DR internally to estimate TTC PDs, (ii) each TTC PD is based on a blended estimation across the data provided by several rating agencies, (iii) the external data is regularly updated to include new publications from rating agencies, and (iv) the decision to use external ratings and PDs is reconsidered by the Model Oversight Committee on a regular basis.
3.5 PIT PD and PD Terms Structure
3.5.1
Modelling choices surrounding PIT PD and PD term structure have material consequences on the estimation of provisions and subsequent management decisions. Several methodologies exist with benefits and drawbacks. The choice of methodology is often the result of a compromise between several dimensions, including but not limited to: (i) rating granularity, (ii) time step granularity and (iii) obligor segmentation granularity. It is generally challenging to produce PD term structures with full granularity in all dimensions. Often, one or two dimensions have to be reduced, i.e. simplified.
3.5.2
Institutions should be aware of this trade-off and should choose the most appropriate method according to the size and risk profile of their books. The suitability of a methodology should be reviewed as part of the validation process. The methodology employed can change with evolving portfolios, risk drivers and modelling techniques. This modelling choice should be substantiated, documented and approved by the Model Oversight Committee. Modelling suggestions made by third party consultants should also be reviewed through a robust governance process.
3.5.3
For the purpose of the MMG, minimum expected practices are articulated for the following common methods. Other methodologies exist and are employed by practitioners. Institutions are encouraged to make research and consider several approaches.
(i) The transition matrix approach, (ii) The portfolio average approach, and (iii)
The Vasicek credit framework.
3.5.4
Irrespective of the modelling approach, institutions should ensure that the results produced by models meet business sense and economic intuition. This is particularly true when using sophisticated modelling techniques. Ultimately, the transformation and the adjustment of data should lead to forecasted PDs that are coherent with the historical default rates experienced by the institution. Deviations should be clearly explained.
3.6 PIT PD with Transition Matrices
3.6.1
This section applies to institutions choosing to use transition matrices as a methodology to model PD term structures.
3.6.2
Transition matrices are convenient tools; however, institutions should be aware of their theoretical limitations and practical challenges. Their design and estimation should follow the decision process outlined in the MMS. Institutions should assess the suitability of this methodology vs. other possible options as part of the model development process. If a third party consultant suggests using transition matrices as a modelling option, institutions should ensure that sufficient analysis is performed, documented and communicated to the Model Oversight Committee prior to choosing such modelling path.
3.6.3
One of the downsides of using transition matrices is the excessive generalization and the lack of industry granularity. To obtain robust matrices, pools of data are often created with obligors from various background (industry, geography and size). This reduces the accuracy of the PD prediction across these dimensions. Consequently, institutions should analyse and document the implications of this dimensionality reduction.
3.6.4
The construction of the TTC matrix should meet a set of properties, that should be clearly defined in advance by the institution. The matrix should be based on the institution’s internal data as it is not recommended to use external data for this purpose. If an institution does not have sufficient internal data to construct a transition matrix, or if the matrix does not meet the following properties, then other methodologies should be considered to develop PD term structures.
3.6.5
At a minimum, the following properties should be analysed, understood and documented:
(i)
Matrix robustness: Enough data should be available to ensure a robust estimation of each rating transition point. Large confidence intervals around each transition probabilities should be avoided. Consequently, institutions should estimate and document these confidence intervals as part of the model development phase. These should be reviewed as part of the model validation phase. (ii)
Matrix size: The size of the transition matrix should be chosen carefully as for the size of a rating scale. A number of buckets that is too small will reduce the accuracy of decision making. A number of buckets that is too large will lead to an unstable matrix and provide a false sense of accuracy. Generally, it is recommended to reduce the size of the transition matrix compared to the full rating scale of the institution. In this case, a suitable interpolation method should be created as a bridge from the reduced matrix size, back to the full rating scale. (iii)
Matrix estimation method: Amongst others, two estimation methods are commonly employed; the cohort approach and the generator approach. The method of choice should be tested, documented and reviewed as part of the model validation process. (iv)
Matrix smoothing: Several inconsistencies often occur in transition matrices, for instance (a) transition probabilities can be zero in some rating buckets, and/or (b) the transition distributions for a given origination rating can be bi-modal. Institutions should ensure that the transition matrix respect Markovian properties.
3.6.6
If the institution decides to proceed with the transition matrix appraoch, the modelling approach should be clearly articulated as a clear sequence of steps to ensure transparency in the decision process. At a minimum, the following sequence should be present in the modelling documentation. The MMG does not intend to elaborate on the exact methodology of each step. Rather, the MMG intends to draw attention to modelling challenges and set minimum expected practices as follows:
(i)
TTC transition matrix: The first step is the estimation of a TTC matrix that meets the properties detailed in the previous article. (ii)
Credit Index: The second step is the construction a Credit Index (“CI”) reflecting appropriately the difference between the observed PIT DR and TTC DR (after probit or logit transformation). The CI should be coherent with the TTC transition matrix. This means that the volatility of the CI should reflect the volatility of the transition matrix through time. For that purpose the CI and the TTC transition matrix should be based on the same data. If not, justification should be provided. (iii)
Forecasted CI: The third step involves forecasting the CI with a macroeconomic model. However, a segmentation issue often arises. If the matrix was created by pooling obligors from several segments, then only one blended CI will be estimated. This may be insufficient to capture the relationship between macroeconomic variables and the creditworthiness of obligors at segment level for the purpose of PIT modelling. Institutions should be cognisant of such limitation and provide solutions to overcome it. An option is to adjust the blended forecasted CI to create several granular CIs that would reflect the behaviour of each segment. (iv)
Adjusted transition matrix: The fourth step is the development of a mechanism to adjust the TTC transition matrix with the forecasted CI or the adjusted CIs. Several forward PIT transition matrices should be obtained at several points in the future. (v)
PD term structure: Finally, a PD term structure should be created based on the forward PIT transition matrices. Methodologies based on matrix multiplication techniques should be robust and consistently applied.
3.6.7
As part of the development process, several pre-implementation validation checks should be performed on the TTC transition matrix in order to verify that the above properties are met. In addition, for each segment being modelled, the matrix should be constructed such that two logical properties are met by the PD outputs:
(i)
The weighted average TTC PD based on the default column of the TTC transition matrix should be reasonably close to the long term default rate of the obligors from the same segment(s) employed to build the matrix. (ii)
The weighted average PIT PD based on the default column of the PIT transition matrix for the next few time steps, should be coherent with the current default rate of the obligors from the same segment(s) employed to build the matrix or the segment(s) employed to derived the adjusted CIs.
3.7 Portfolio Scaling Approach
3.7.1
This section applies to institutions using a portfolio-level scaling approach to model the term structure of PIT PD. This approach is simpler to implement than transition matrices and is suitable for portfolios with smaller data sets. In this method, average PD across ratings are being modelled, instead of all transition points between ratings. This approach tends to be preferred for smaller segments. The obligor segmentation granularity is preserved at the expense of a simplification of the rating granularity.
3.7.2
In order to ensure transparency in the decision process, the modelling approach should be clearly articulated as a clear sequence of steps. It is not the object of the MMG to elaborate on the exact methodology of each step. Rather, the MMG intends to draw attention to modelling challenges and set minimum expected practices. At a minimum, the following sequence should be present in the modelling documentation:
(i) Forecast portfolio average PIT PD per segment based on macro-PD models. (ii) Estimate the deviation of the portfolio PIT PD from its long term average PD. (iii)
Apply this deviation to PDs at lower granularity levels, for instance pools or rating grades. This can be achieved by scaling in logit or probit space. (iv)
Construct a PIT PD term structure. It is highly recommended to compare several methods and test their impacts on PD outcomes and risk metrics.
3.7.3
The drawback of this method is the generalisation of the PD volatility across grades (or pools) with the use of scalers. Certain rating grades are more prone to volatility than others, which is not reflected in this type of model. Therefore this method could result in an underestimation of the PIT PD of the lowest rating grades. Consequently, institutions should demonstrate that they assess and understand this effect.
3.7.4
Institutions should ensure that scalers lead to explainable shifts of the PD curve across rating grades and across time steps. The scalers will not be static. They will change through the forecasted time steps, since they follow the path of the PD forecasts.
3.7.5
Institutions should be aware of the theoretical and practical limitations of this approach. Its design and estimation should follow the decision process outlined in the MMS. As for any other models, institutions should assess the suitability of this methodology vs. other possible options as part of the model development process.
3.8 The Vasicek Credit Framework
3.8.1
The Vasicek credit framework is sometimes used to model PIT PD term structures. Institutions should be cognisant of the material challenges arising from using the Vasicek one-factor credit model (or similar derivations) for the purpose of ECL estimation, for the following reasons:
(i)
This model has been originally designed to model economic capital and extreme losses at portfolio level. It is designed to replicate the behaviour of credit risk for a granular and homogeneous portfolio. Whilst it is an elegant modelling construction, it might not be the most suitable approach to model expected loss behaviours at the level of individual obligors. (ii)
It relies on parameters that are challenging to calibrate, in particular the asset correlation representing the correlation between (a) obligors’ asset value and (b) a non-observable systemic factor - generally assimilated to an industry factor for practical reasons. The model results are highly sensitive to the choice of this parameter. When modelling PIT PD, the introduction of this correlation parameter tends to reduce the impact of macroeconomic factors. (iii)
When it is used for ECL, the Vasicek model is often combined with a macroeconomic regression model. In this case, the non-observable systemic factor is not a given input. Rather, it is partially driven by macro variables. Consequently, the commonly used one- factor model should be adjusted to account for the variance of the residuals, i.e. the part of the systemic factor that is not explained by the macro variables.
3.8.2
If an institution decides to use this methodology, this choice should be approved by the Model Oversight Committee, with a clearly documented rationale. The asset correlation parameters should be chosen carefully, bearing in mind the following principle: the lower the PD, the higher the asset correlation because the obligor’s performance is expected to be mostly driven by systemic factors rather than by idiosyncratic factors.
3.8.3
It is common practice to calibrate the asset correlation based on the values suggested by the Basel Framework employed for capital calculation. However, institutions should consider the possibility that the interconnectedness of corporates in the UAE could lead to higher systemic correlations for some industries. Consequently, institutions should, at a minimum, perform sensitivity analysis to assess the implications of this calibration uncertainty on PDs.
3.9 Validation of PD Models
3.9.1
Irrespective of their choice of methods, institutions should validate PD models according to the principles articulated in the MMS. In particular for PD models, both qualitative and quantitative assessments are required.
3.9.2
Institutions should ensure that the following metrics represent accurately the risk profile of their books at segment-level: TTC 1y PD, PIT 1y PD and PD term structure. For that purpose, these metrics should be validated at several granularity levels (e.g. rating grades, segments, industries). Statistical tests alone are generally not sufficient to conduct appropriate validation of PD at segment level. Consequently, institutions should combine statistical tests, judgement and checks across several metrics to ensure that the calibration of these metrics are meaningful and accurate.
3.9.3
Comprehensive techniques should be developed in order to validate PIT PDs. At a minimum, institutions and their supporting third parties should cover the comparisons articulated in the following table. This logical cross-check approach involves comparing variables estimated via several methods. In addition to these comparisons, institutions should design and compute other metrics to suit their specific PD methodology.
3.9.4
If insufficient data is available to estimate some of the metrics in the below table, institutions should demonstrate that actions are taken to collect data to produce these metrics. Given the lack of data, they should also explain their approach to assess the suitability of the PIT PD calibration currently used in production.
Table 2: Metrics used to validate PD models
Segment level metrics Point-in-Time metrics (PIT) Through-the-Cycle metrics (TTC) 1-year Default Rate
(“1y DR”)PIT 1y DR are historically observed default rates per segment. Should be in a form a rolling time series, preferably with monthly intervals. TTC 1y DR are computed as the average of PIT 1y DR through time. They can be weighted by the number of performing obligors in each time step. Cumulative Default Rate
(“CDR”)PIT CDR are historically observed default rates over several performance windows, covering for instance 2, 3 and 4 years. The result should be several term-structures of defaults, observed at several points in time. Also computed per segment. TTC CDR is the average of the CDR through time, per performance window, covering for instance 2, 3 and 4 years. The result should be a single PD term structure of default per segment. 1-year Probability of Default
(“1y PD”)PIT 1y PD estimated based on score-to-PD calibration and macro models. Estimated at segment level as the average across rating grades (exposure-weighted or count-weighted). TTC 1y PD can be computed with several methods. For instance as: (i) weighted average PD based on the bank’s master scale, or (ii) if transition matrices are used, weighted average across the default column of the TTC matrix. Cumulative Probability of Default (“CPD”) Terms structure of PIT PD per segment and rating grades produced by models. Estimated per segment as the average across rating grades (exposure-weighted or count-weighted). Not always available, depending on the methodology. In the case of transition matrices, it should be based on the TTC matrix computed over several time horizons. 3.9.5
Upon the estimation of the above metrics, institutions should perform the following comparisons at segment level. Institutions should implement acceptable limits to monitor each of the following comparison, i.e. the difference between each two quantities. These limits should be included in the model validation framework and agreed by the Model Oversight Committee. Frequent and material breaches should trigger actions as articulated in the governance section of the MMS.
(i)
TTC 1y DR vs. TTC 1y PD per segment: The objective is to verify that the central tendency observed historically is in line with the PD estimated based on the institution’s master-scale. (ii)
PIT 1y DR vs. PIT 1y PD estimated over the same historical period, per segment: This is a back testing exercise. The objective is to verify that the default rates observed historically are falling within a reasonable confidence interval around the PD forecasted over the same period. (iii)
PIT 1y DR recently computed vs. PIT 1y PD estimated over the next 12 months: The objective is to verify that the default rate recently observed is coherent with the PD forecasted from the reporting date over the next 12 months. These two quantities can diverge due to the effect of economic forecasts. There should be a logical and intuitive link between the two and material differences should be explained. (iv)
TTC CDR vs. PIT CPD per segment: The objective is to verify that the shape of the cumulative default rates observed historically is similar with the shape of the cumulative default rate forecasted by the model from the portfolio reporting date. The shape can be expressed as a multiplier of the 1-year PD. (v)
TTC CDR vs. PIT PD derived analytically: A PD term structures can be estimated simply by using survival probabilities derived from the institution’s PD mater scale. This is referred as the analytical PD term structure, that serves as a theoretical benchmark. The objective is to compare this analytical benchmark vs. (a) observed CDR and (b) the PD term structure generated by the model. Material deviations should be understood and documented. If CDR and CPD are materially lower than the analytical approach, adjustments should be considered.
3.9.6
In addition to segment level validation, institutions should ensure that the PIT PD profile across rating grades is logical and consistent. This is particularly relevant in the case of transition matrices. PIT adjustments should be coherent across different ratings. Technically, for a given segment and a given horizon forecast, the log-odd ratio of the PIT PD for a given rating over the TTC PD for the same rating, should be of similar magnitude between ratings.
3.9.7
Finally, economic consistency between segments is also part of the validation process of PD models. Institutions should ensure that such considerations are included in the scope of model validation. PIT PDs generated by models should be coherent between industries and between segments. For instance, if a given portfolio displayed high historical PD volatility, then such volatility is expected to be reflected in the forecasted PIT PD. Material deviations from coherent expectations should be explained and documented.