5 Macroeconomic Models
5.1 Scope
5.1.1
Macroeconomic models (“macro models”) are primarily employed by UAE institutions for the estimation of Expected Credit Loss (“ECL”) and for internal and regulatory stress testing purpose. The objective of this section is to provide guidance and set the Central Bank’s expectation applicable to all macroeconomic models used by institutions. The practices described in this section are in compliance with current accounting principles.
5.1.2
In this context, macro models are defined as statistical constructions linking macro variables (“independent variables”) to an observed risk or business metrics, typically PD, Credit Index, LGD, cost of funds, or revenues (“dependent variables”). Several types of macro models exist. A common approach relies on time series regression techniques, which is the main focus of this section on macro models. Other approaches include (i) for retail clients, vintage-level logistic regression models using directly macroeconomic drivers as inputs and (ii) for corporate clients, structural models using macro variables as inputs.
5.1.3
Irrespective of the methodology employed, institutions should use judgement and critical thinking, where statistical techniques are coupled with causality analysis. Institutions should justify and balance (i) statistical performance, (ii) business intuition, (iii) economic meaning, and (iv) implementation constraints. Statistical methods and procedures will only provide part of the solution. Therefore, rigorous modelling techniques should be coupled with sound economic and business judgement in order to build and choose the most appropriate models. The key modelling choices and the thought process for model selection should be rigorously documented and presented to the Model Oversight Committee.
5.1.4
The modelling decision process should be driven by explorations, investigations, and comparisons between several possible methods. Note that time series regression models have been proven to yield the most intuitive results over other techniques.
5.1.5
When developing macro models, institutions should follow a clear sequential approach with a waterfall of steps. Depending on the outcome, some steps may need to be repeated. Each step should be documented and subsequently independently validated. In particular, for time series regression models, the process should include, at a minimum, the steps presented in the table below.
Table 8: Sequential steps for the development of macro models
# Step 1 Data collection 2 Analysis of the dependent variables 3 Analysis of the macro variables 4 Variable transformations 5 Correlation analysis 6 Model construction 7 Statistical tests 8 Model selection 9 Monitoring and validation 10 Scenario forecasting 5.2 Data Collection
5.2.1
In order to proceed with macroeconomic modelling, institutions should collect several types of time series. This data collection process should follow the requirements articulated in the MMS.
5.2.2
At a minimum, these time series should be built with monthly or quarterly time steps over an overall period of five (5) years covering, at least, one economic cycle. Institutions should aim to build longer data series. The following data should be collected.
5.2.3
Macro variables: Institutions should obtain macro variables from one or several external reliable sources.
(i)
The scope of variables should be broad and capture appropriately the evolution of the economic environment. They will typically include national accounts (overall and non-oil, nominal and real), oil production, real estate sector variables, CPI, crude oil price and stock price indexes. (ii)
Institutions should collect macro data pertaining to all jurisdictions where they have material exposures (at least greater than ten percent (10%) of the total lending book, excluding governments and financial institutions). (iii)
Institutions should document the nature of the collected variables, covering at a minimum, for each variable, a clear definition, its unit, currency, source, frequency, and extraction date. (iv)
Institutions should ensure that all variables employed for modelling will also be available for forecasting.
5.2.4
Historical default rates: Macro-PD models (or macro-to-credit index models) stand at the end of a chain of models. They are employed to make adjustments to the output of TTC PD models, themselves linked to rating models. Therefore the default data used for macro-PD modelling should reflect the institution’s own experience. If external default data points are used, justification should be provided. Finally, institutions are encouraged to also include restructuring and/or rescheduling events in their data to better capture the relationship between obligor creditworthiness and the economic environment.
5.2.5
Historical recovery rates: Macro-LGD models are designed to adjust the output of TTC LGD models. Consequently, the recovery data employed for macro-LGD modelling should reflect the institution’s own experience. If external recovery data points are used, justification should be provided.
5.2.6
Macro data series are mostly available with quarterly or even annual data points and rarely with monthly time intervals. Consequently, interpolation techniques may need to be developed. Institution should include interpolation methodology as part of the data transformation step. Such interpolation should be documented and included in the validation process.
5.3 Analysis of the Dependent Variables
5.3.1
Institutions should demonstrate that default series are suitable for modelling and are representative of their current portfolio. For that purpose, they should employ judgement and critical thinking when analysing the data. At a minimum, they should perform an analysis of the dependent variables through descriptive statistics, covering the distribution followed by each dependent variable and the identification of outliers, if any. Upon this analysis, a clear statement should be made regarding the suitability of the data for macro modelling. Consideration should be given to (i) the data quality, (ii) length, and (iii) representativeness. This analysis should be fully described in the model development documentation.
Business consistency: Institutions should pay attention to the business significance of the historical data related to the dependent variable. One possible conclusion is that historical data of a given variable is no longer an appropriate representation of the current institution’s portfolio because the segment business strategy has changed materially. In the case of default and recovery rates, conservatism prevails.
(i)
The institution may believe that its current portfolio is less risky than its historical portfolio and that it expects to experience lower default rates and/or losses in the future. In that case, the existing historical default series should be used for a reasonable period until there is enough evidence supporting the new risk profile. Subsequently, adjustments are permitted on the forecasted values, for instance in the form of scalers. (ii)
The institutions may believe that its current portfolio is more risky than its historical portfolios and that it will consequently experience higher default rates in the future. In that case, forecasts should be immediately adjusted, i.e. forecasted PDs and LGDs should be shifted upward.
5.3.2
Regime shifts: Institutions should identify the presence of regime shifts in all times series. These can be clearly identified by the presence of sudden permanent jumps in the data. Regime shifts tend to occur in default and recovery series due to changes in the data collection process, definition of default, recovery process or business strategies. For modelling, it is strongly recommended to avoid using time series with regime shifts as direct model inputs. Instead, adjustments should be implemented such as a truncation of the series or the use of specific econometrics techniques (the introduction of a dummy variable in the model).
5.3.3
Segmentation consistency: Segmentation means splitting a statistical sample into several groups in order to improve the accuracy of modelling. This concept applies to any population of products or customers. In particular, for the construction of PD and LGD macro models, the choice of portfolio, customer and/or product segmentation has a material impact of the quality of macro models. The economic behaviours of obligors and/or products should be homogeneous within each segment in order to build appropriate models. As mentioned in the data collection section, a degree of consistency is required between macro models and other models. For macro-PD models in particular, such consistency should be analysed and documented as follows:
(i)
The granularity of segments for macro modelling should be equal or greater than the granularity of segments employed for (i) rating models, and (ii) PD term structures models. If this alignment is not possible, institutions should provide robust justifications and document them accordingly. (ii)
Institutions may decide to increase the segmentation granularity of macro models. An increase in the number of segments will lead to a reduction in segment size and in the number of observed defaults, could, in turn, reduce the statistical significance of the default rate. Therefore, increasing the segmentation granularity is permitted, provided that there is no material loss in the representativeness of the default rates.
5.3.4
Institutions should analyse and assess the impact of segmentation choices as part of the development of macro models. Several segmentation options should be considered and subject to the entire model development process described hereby. Institutions should then choose the best segmentation by assessing the quality and robustness of the macro models across several segmentation options.
5.4 Analysis of the Macro Variables
5.4.1
Institutions should perform a robust analysis of the macro variables through descriptive statistics. At minimum, this analysis should examine, amongst others, the shape of distribution to identify outliers, shape of tails, multimodality. Upon this analysis, a clear statement should be made regarding the suitability of the data for macro modelling. In particular, the analysis should consider the data quality, length and representativeness. This analysis should be fully described in the model development documentation.
5.4.2
Regime shift: Institutions should identify the presence of regime shifts in all macro time series. Regime shifts can occur in macro time series due to economic decisions such as the introduction of VAT or a large shift in interest rates. Similarly to the dependent variables, macro time series with regime shifts should be avoided or adjusted accordingly.
5.4.3
Economic consistency: Institutions should pay attention to the economic significance of the macro variables. Some macro variables provide consistently better explanatory power of risk metrics in the banking book. Conversely some variables are more challenging to interpret, consequently institutions should be cautious when using those variables for PD and LGD macro models. Particular attention is needed for the following:
(i)
Employment rate: A large proportion of employees leave the UAE upon losing their employment. Consequently, the UAE employment rate incorporates a material bias, hence it is preferable to avoid this variable to model business or risk metrics. (ii)
Interest rates: The relationship between interest rates and default rates is ambiguous. Institutions should ensure that an appropriate interpretation of the estimates is provided upon modelling PDs and LGDs. (iii)
Abu Dhabi and Dubai stock indices: These indices can suffer from a lack of liquidity therefore institutions should ensure that an appropriate interpretation of the estimates is provided upon modelling PDs and LGDs. (iv)
UAE account balances (e.g. fiscal balance, current account): By construction these variables can oscillate between positive and negative values. Consequently, a relative time differencing can lead to very high returns and uncontrollable spikes. Instead, it is recommended to normalise these variables by nominal GDP prior to using them for modelling.
5.5 Variable Transformations
5.5.1
The principles of variable transformation articulated in the MMS also apply to macro models. Variable transformations have a material impact on macro models and on ECL. Therefore, institutions should test, choose and document the most appropriate transformations applied to both the macro variables and to the dependent variable.
5.5.2
Stationarity: Modelled economic relationship should be stable over time. In the context of time series regression model, variables should be stationary in order to construct robust and meaningful econometric models. Stochastic trends, seasonality and structural breaks are most common sources of non-stationarity. This property should be tested for both the dependent and independent variables, according to the following principles:
(i)
Macroeconomic variables should meet stationarity criteria prior to be used for modelling. The absence of stationarity has adverse material consequences on macro models because it often leads to spurious correlations. Macro variables that are not stationary should either be transformed to obtain stationary series or should be excluded from the modelling process. (ii)
Even after transformations, in some circumstances full stationarity is challenging to obtain if series are short and data is scarce. In this case, institutions should use judgement and critical thinking to balance economic significance and stationarity requirement in order to assess if modelling can proceed. In this assessment, institutions should pay particular attention to the presence of trends, that often leads to spurious correlations. (iii)
To test for stationarity, standard unit root test may be used, including the Augmented Dickey-Fuller test, the Phillips-Perron test, the Kwiatkowski-Phillips-Schmidt-Shin (KPSS test). In case there is evidence of the presence of stochastic trend, standard transformations can be applied such as quarter-on-quarter or year-on-year log differencing. (iv)
Seasonality may be checked using X12 or X13 seasonal adjustment algorithms. Year-on-year differencing could also be used to remove stable seasonal patterns. Formal structural breaks tests (e.g. Chow test) may be employed if there is visual evidence of break in the series. (v)
Common stochastic trends between two variables may be explicitly modelled using the rigorous application of standard co-integration models (e.g. Engle-Granger two step method or Johansen approach). (vi)
The absence of stationarity of the dependent variable can also be addressed by a first order time differencing or by autoregressive models. However, this can potentially lead to further complexity in implementation. Institutions should use judgement in this choice provided that it is justified and clearly documented.
5.5.3
Differencing: Time differencing should be based upon the following principle. Let Xt be a time series of the macroeconomic variable X at regular time steps t. Formally we can define two types of changes: (i) backward looking returns that estimate the change of the variable over a previous horizon h and (ii) forward looking returns that estimate the change of the variable over a coming horizon h. Formally:
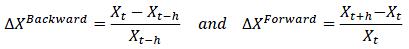
It is recommended to build macro models based on backward looking returns as these are more intuitive to interpret and easier to implement. It is also recommended to compute backward looking default rates in order to ensure that both the dependent and independent variables are homogeneous.
5.5.4
Horizon of differencing: Institutions should choose carefully the horizon of return applied to macro variables, i.e. the period used to compute the change of a variable through time. Institutions should take notes of the following principles:
(i)
For macroeconomic models, common return horizons include quarterly, half-yearly and yearly. The most appropriate return horizon should be chosen to maximize the explanatory power of the macro variables. (ii)
Note that the return horizon is not necessarily equal to the granularity of the time series. For instance, rolling yearly returns can be computed on quarterly time steps. (iii)
Institutions should be aware of the degree of noise in high frequency data. Consequently judgement should be used when using high frequency returns.
5.5.5
Lags: Variable lags should be considered in the modelling process to capture delayed effects of macro drivers. The use of large lags (more than 6 quarters) should be justified since long lags delay the impact of macro shocks on the dependent variable. For each macro variable, the choice of the most appropriate lag should be based on its statistical performance and economic meaning.
5.5.6
Smoothing: This means reducing the presence of spikes and outliers in times series. This is commonly addressed by the usage of moving average. Such practice is permitted but should be employed with caution and documented. The right balance of smoothing needs to be found. No smoothing (too much noise) in time series can lead to weak models. Alternatively, too much smoothing can dilute the strength of correlations. Smoothing techniques should be documented when applied.
5.5.7
Standard and intuitive transformations should be used. For example, the growth rate of a variable that can be zero or negative is not a meaningful measure.
5.6 Correlation Analysis
5.6.1
The objective of the correlation analysis is to assess the strength of the relationship between (i) each of the transformed dependent variable (e.g. PD) and (ii) each of the transformed macro variables, on a bilateral basis. Consequently such univariate analysis should be performed for each obligor segment. This analysis should include both statistical and causality perspectives. Relationships should make economic sense and meet business intuitions.
5.6.2
Institutions should pay attention to the strength and sign of correlations (positive vs. negative relationships) and assess whether they meet business intuitions. At a minimum, the following components should be documented: (i) the top macro variables ranked by correlation strength and (ii) comments and analysis on the observed statistical relationships vs. expected business intuitions.
5.6.3
A cut-off should be establish to eliminate the transformed macro variables that display weak and/or incoherent correlations with the independent variables. This reduced population of transformed macro variables should be used to perform multivariate analysis.
5.7 Model Construction
5.7.1
The objective of this step is to construct relevant and robust relationships between a single transformed dependent variable (e.g. PD) and several macro variables. The choice of the macro variables entering each model should be based upon the results of the correlation analysis. This process results in the construction of a range of multifactor models for each dependent variable.
5.7.2
In the context of time series regressions, institutions should choose the most appropriate methodology to perform multifactor regressions. Amongst others, it is recommended to perform multifactor regressions with or without autoregressive terms. It is recommended that institutions include several modelling forms as part the pool of possible model candidates.
5.7.3
The estimation of model coefficients should be performed with recognised professional statistical software and packages. The entire process should be fully documented and replicable by an independent party.
5.7.4
Several performance metrics should be used to rank and choose models. As these metrics depend on the type of models, institutions should use judgements to employ the most appropriate performance metrics per model type. At a minimum, the adjusted R-square should be used for multifactor regression models. For models based on the ARIMA form, a pseudo R-square should be employed as the square of the correlation between the fitted variable and the original dependent variable.
5.8 Statistical Tests
5.8.1
Standard post-estimation tests should be used to check that the underlying assumptions are appropriate for all types of macro models. The set of appropriate tests should be based on best practices in the relevant field / literature. The model development documentation should clearly indicate (i) the chosen test for each property, (ii) the nature of the H0 hypothesis, (iii) the cut-off values chosen upfront to determine the rejection or non-rejection.
5.8.2
In the context of time series regression, regression coefficients should be significant and residuals should be tested for autocorrelation and normality. The table below indicates properties that should be tested, at a minimum. Other tests may be considered, if necessary.
Table 9: Typical statistical tests for models based on time series regression
Property to be tested Description of the property to be rejected Suggested test (others may exist) Stationarity Absence of stationarity in each time series Augmented Dickey-Fuller (ADF) Co-integration Absence of stationarity in a linear combination of the dependent variable and each independent variable Engle-granger two-step method Multicolinearity High correlation between the independent variables Variance Inflation Factor Coefficient significance The coefficients are not statistically significantly different from zero Coefficient p-value on a t-distribution Autocorrelation High correlation between the error terms of the model Ljung-Box test Heteroscedasticity Absence of relationship between independent variables and residuals Breusch-Pagan or White test Normality Normal distribution of the residuals Shapiro Wilk 5.9 Model Selection
5.9.1
The model and macroeconomic variable selection should be based on clearly defined performance criteria using a transparent selection algorithm. The final model should be able to (i) generate values that fit the historical values of the dependent variable and (ii) generate accurate predictions.
5.9.2
For each segment, institutions should choose a final model from the list of candidate models generated from the model construction step. Statistical performance should not be the only decisive factor to choose a model. Instead, the choice of the final model should be based upon the combination of various factors. At a minimum, institutions should use the criteria outlined below. It is essential that institutions include all these criteria in the selection process. The absence of one criteria could be materially detrimental to the choice of the most relevant model.
(i)
Statistical performance:
a.
The chosen model should meet minimum requirements of performance, statistical stability and robustness as shown by the statistical indicators and their associated thresholds. Model parameters and forecasts should remain stable over time. b.
In addition, at the model development stage, it is important to examine the stability of models: out-of-sample performance and in-sample fit should be tested and compared across candidate models. A common metric employed to express model performance is the root mean square error, for which limits should be established.
(ii)
Model sensitivity: Quantitative response of the dependent variable to independent variables should be meaningful and statistically significant - both quantitatively and qualitatively. This can be examined through simulating one standard deviation change in individual dependent variables or by considering the forecast differences across alternative scenarios. (iii)
Business intuition: The chosen model should be constructed with variables and relationships that meet logical business and economic intuitions. This means that the model should be explained by causal relationships. (iv)
Realistic outcomes: Projected values should be consistent with historical observations and meet economic intuition. Any material jump and/or disconnect between historical values and forecasted should be explained. (v)
Implementation: When choosing a model, institutions should be mindful of the implementation and maintenance constraints, which should form part of the choice of the most appropriate models. For instance, some variables may not be available as frequently as expected for forecasting. Also, some model formulations may require autoregressive terms that need specific treatment during implementation.
5.9.3
In order to test the business intuition, for each candidate model, institutions should forecast the dependent variables (e.g. PD, Credit Index) under a severe downside scenario. The outcome will therefore be a range of projected dependent variables (one for each model) under the same scenario. It may become apparent that some candidate models should be excluded as they generate outputs that deviate too much from economic and business expectations.
5.9.4
Forecast Uncertainty: Projected forecast are based on mean or median values, around which uncertainty (i.e. confidence interval) inherently exists. Institutions should ensure that the model forecast uncertainty are clearly estimated, documented and reported to the Model Oversight Committee. In the context of time series regression, the confidence interval around the mean can be estimated empirically or based on the standard deviation of the residuals under the assumption of normally distributed residuals.
5.10 Validation of Macro Models
5.10.1
The validation of macro models should be performed by a different and independent party from the development team, according to the validation principles articulated in the MMS. If macro models are developed by a third party consultant, then a team within the institution or another consultant should therefore perform these independent validations.
5.10.2
Monitoring macro models may be challenging due to the low frequency of macroeconomic data. Institutions are expected to monitor the performance of macro models once a year. However, exceptional monitoring is required in the case of exceptional macroeconomic events.
5.10.3
Pre-implementation validation: This step involves the validation of the chosen macro models immediately after their development, prior to using them in production. The objective is to ensure that macro models meet a minimum level of quality and that they are fit for purpose. At a minimum, the following validation steps should be performed.
(i)
Development process: The validator should review the development process as per the principles articulated in the MMS. (ii)
Replication: The validator should replicate the final chosen model per segment and ensure that the coefficients are correctly estimated. (iii)
Statistical tests: The validator should ensure that statistical tests are correct, that cut-offs are reasonable and that statistical assumptions are correctly interpreted. This may necessitate partial replication. Additional statistical tests may be needed. (iv)
Model sensitivity: The validator should measure the elasticity of the model output to changes in each input variable. The model user and validator should be aware of the presence of independent variables that dominates other variables in a given model. (v)
Model stability: The validator should test the model stability, for instance by removing data points from the original time series (at the start or the end), re-run the regressions and re-project the dependent variable. The validator should also examine the stability of the model coefficients. (vi)
Conclusion: When deemed appropriate, the validator can make suggestions for defect remediation to be considered by the development team.
5.10.4
Post-usage validation: This is otherwise referred to as back-testing, whereby the validator should compare the realized values of the dependent variable (e.g. PD, LGD, Credit Index) against the forecasted values based on the macroeconomic scenarios employed at the time of the forecast. A conclusion should be made based pre-defined confidence intervals.
5.10.5
Upon the post-usage validation, the validator should make a clear statement regarding the suitability of the model to be used for another cycle. When deemed appropriate, the validator can make suggestions for defect remediation to be considered by the development team.
5.11 Scenario Forecasting
5.11.1
The expected practices articulated in this section relate to the regular estimation of ECL. As per current accounting requirements, institutions should estimate an unbiased and probability weighted ECL by evaluating a range of possible outcomes. Consequently, institutions should forecast economic conditions over the lifetime of their portfolio. All the macroeconomic variables employed as input in macro models should be forecasted until the longest maturity date of the institutions’ portfolio.
5.11.2
Institutions are encouraged to disclose macroeconomic scenarios in their annual reports. For this information to be meaningful, institutions should provide the values of the main economic drivers over the next three (3) years with the weight of each scenario.
5.11.3
Institutions should use the most recent set of models to forecast PD and LGD. If the most recent models are not used in the computation of ECL, this should be mentioned in monitoring and validation reports and reported to internal and external auditors because it has direct impacts on financial reporting.
5.11.4
Governance: Institutions can either develop macroeconomic forecasts internally or rely on third party providers. In both cases, a governance process should be put in place to guarantee the quality of forecasts.
(i)
If scenarios are developed internally, they should be constructed by subject matter experts with robust economic knowledge, within the institution. The scenarios should be reviewed by the Model Oversight Committee and the committee in charge of ECL oversight. (ii)
If scenarios are developed externally, institutions should put in place an internal validation process, by which the forecasts are checked, errors are adjusted and economic consistency is ensured. Even if scenarios are provided by an external party, each institution remains the owner of the economic forecasts and therefore remains accountable for inconsistencies present in those scenarios. (iii)
To support the adequate estimation of ECL, institutions should produce regular reports to present the aspects of macro scenario calibration discussed in this section. The report should address the source of scenarios, their economic consistency, their severity, weights and potential adjustments.
5.11.5
Weights and severity: As per current accounting requirements, institutions should use several weighed scenarios. At a minimum, institutions should employ one base, one upside and one downside scenario for each macro variable. In order to obtain an unbiased estimation of ECL, both the scenario weights and their associated severity should be jointly calibrated. For each variable, institutions should pay attention to the relative weight and severity of the downside scenario vs. the weight and severity of the upside scenario. Finally, it is recommended to estimate the ECL under each scenario in order to convey possible ECL volatility and support appropriate risk management.
5.11.6
Forward looking information: As per current accounting requirements, ECL should be based on forward looking information that is relevant reasonable and supportable. This should be understood as follows:
(i)
The economic information should be based on consensus, when possible, rather than a single source. (ii)
The economic forecasts should be realistic in terms of trend, level and volatility. For instance, economic forecasts assuming a constant positive inflation should not push asset prices to excessive and unrealistic levels in the long term. This feature is particularly relevant for real estate collaterals. (iii)
The divergence between the scenarios (base, upside, downside) should meet economic intuition and business sense. Such divergence should follow a logical economic narrative.
5.11.7
Benchmarks: Aside from ECL measurement, institutions employ existing scenarios for planning purposes, with varying severity and probability of occurrence. Amongst others, dedicated scenarios are used for the ICAAP, the recovery and resolution plan, and for stress testing purpose. These scenarios should not be employed as input for ECL computation because they do not represent an unbiased probability-weighted set of scenarios. Similarly, the macroeconomic scenarios provided by the CBUAE as part of regulatory enterprise-wide stress testing exercises should not be used as input for ECL computation. All these alternative scenarios can only be used as distant comparables for the ECL scenarios. However, this comparison should be made with caution because the calibration (severity, likelihood) of the ECL scenarios is likely to be different.
5.11.8
The construction of the scenarios should be economically coherent and therefore should follow a set of rules to be consistent. Let Xt be a time series of the macroeconomic variable X at regular time steps t. For the purpose of articulating this point, we will use three scenarios. The time series of X corresponding to each scenario are noted Xtbase, XtUp and XtDown .
(i)
Scenarios should be constructed in such way that their values diverge after a given date, called the forecasting date, noted T. The time series for the three scenarios should be identical prior to the date of forecast and diverge after the date of forecast. Formally:
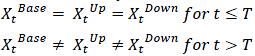
(ii)
The portfolio date noted K employed in loss computation should be close to the forecasting date. Therefore, institutions should keep updating the macroeconomic forecasts along with the portfolio date, in order to minimize the time difference between T and K. It may happen that ECL reporting is done at a higher frequency than the update of macroeconomic forecasts. In this case, the time step at which scenarios start diverging occurs before the portfolio date K. Formally, for T<K:
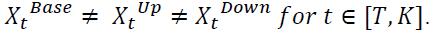
This misalignment is likely to create unwarranted effects in particular if scalers are used in PD modelling. Therefore, the maximum delay between the two dates should be no more than three months: K - T ≤ 3 months. If this difference is greater than three (3) months, the impact on the forecasted PD and LGD should be analysed and documented by the independent model validation team. (iii)
Beyond the forecasting start date, the upside and downside scenarios should not be constructed by a constant parallel shift (or scaling) of the base scenarios. Rather, the upside and downside scenarios should be constructed such that they display a gradual divergence from the base scenario through time (in growth rate terms if growth rates are applied). This property should apply to the stationary transformed macroeconomic variable. Consequently, the forecasted PD and LGD should follow the same pattern. Formally:
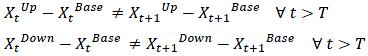
(iv)
Any scaler subsequently constructed based on these scenarios should follow the same pattern: a gradual divergence from the base scenario.
5.11.9
The principles articulated in this section about scenario forecast should also be included in the scope of review of the validation process. The validation process should test, assess and document practices for scenarios forecasts, including the governance, scenario construction and calibration.